Chuck Huber, Director Asociado de Alcance Estadístico.
En
mi última publicación, aprendimos cómo importar los datos
sin procesar de COVID-19 del repositorio GitHub de Johns Hopkins y convertir los datos sin procesar
en datos de series temporales. Esta publicación demostrará cómo descargar datos
en bruto y crear mapas coropléticos como la figura 1.
Figura 1: Casos confirmados de
COVID-19 en los Estados Unidos, ajustados por tamaño de población.
Un
mapa coroplético muestra información estadística sobre áreas geográficas
utilizando diferentes colores o intensidad de sombreado. La Figura 1 muestra el
número ajustado por la población de casos confirmados de COVID-19 para cada
condado en los Estados Unidos a partir del 2 de abril de 2020. Cada tono de
azul en el mapa representa el rango del número de casos que se muestran en la
leyenda inferior izquierda del mapa. Utilicé el comando grmap
contribuido por la comunidad para crear la figura 1, y necesitamos tres datos
sobre cada condado para crear este mapa. Necesitamos la información geográfica
de cada condado, el número de casos confirmados en cada condado y la población
de cada condado.
Comencemos
por el final y avancemos hacia atrás para aprender cómo construir un conjunto
de datos que contenga esta información. Los datos enlistados a continuación se
utilizaron para crear el mapa en la figura 1. Cada observación contiene
información sobre un condado individual en los Estados Unidos.
Las primeras cuatro variables
contienen información geográfica sobre cada condado. La variable _ID contiene un número de
identificación único para cada condado que se utiliza para vincular con un
archivo especial llamado "shapefile". Los shapefiles
contienen la información que se utiliza para representar el mapa y se
explicarán a continuación. La variable GEOID es un código de condado del Estándar Federal de Procesamiento de
Información (FIPS). Podemos usar el código FIPS como una variable clave para
fusionar datos de otros archivos. Las variables _CX y _CY contienen coordenadas geográficas. Podemos descargar estos datos de la Oficina
del Censo de los Estados Unidos.
La variable confirmed contiene el número de casos
confirmados de COVID-19 en cada condado. Estos datos se descargaron del repositorio
GitHub Johns Hopkins. Este no es el mismo archivo que
utilizamos en mis publicaciones anteriores.
La variable confirmed_adj contiene el número de casos
confirmados por 100,000 habitantes. Esta variable se calcula dividiendo el
número de casos para cada condado en confirmed entre la población total para cada condado en popestimate2019. El resultado se multiplica por 100,000 para convertirlo en "casos
por 100,000 habitantes".
Tendremos que descargar datos de
tres fuentes diferentes y fusionar estos archivos en un solo conjunto de datos
para construir el conjunto de datos para nuestro mapa. Comencemos descargando y
procesando cada uno de estos conjuntos de datos.
Lista de temas
Descargue
y prepare los datos geográficos
Descargue
y prepare los datos del caso
Descargar
y preparar los datos de la población
Cómo
fusionar los archivos y calcular recuentos ajustados
Cómo
crear el mapa coroplético con grmap
Descargue y prepare los datos geográficos
Comencemos con los datos geográficos. Los shapefiles
contienen la información geográfica que grmap usa para crear mapas. Muchos shapefiles
están disponibles gratuitamente en internet, y puede localizarlos utilizando un
motor de búsqueda. Por ejemplo, busqué los términos "united states
shapefile", y el primer resultado me llevó a la Oficina del Censo de los
Estados Unidos. Este sitio web contiene shapefiles para los
Estados Unidos que muestran los límites de los estados, distritos del Congreso,
áreas estadísticas metropolitanas, micropolitanas y muchos otros. Me gustaría
subdividir mi mapa de los Estados Unidos por condado, así que me desplacé hacia
abajo hasta que encontré el título "County". Me gustaria usar
el archivo cb_2018_us_county_500k.zip.

Podemos copiar el archivo desde el sitio web a
nuestra unidad local y usar unzipfile para extraer el
contenido del archivo. Puede hacer clic con el botón derecho en el archivo en
la página web, seleccionar "Copiar dirección de enlace" y pegar la
ruta y el nombre de archivo en su comando copy.
Los archivos cb_2018_us_county_500k.shp y cb_2018_us_county_500k.dbf contienen la
información geográfica que necesitamos. Podemos usar spshape2dta para procesar la
información en estos archivos y crear dos conjuntos de datos Stata llamados
usacounties_shp.dta y usacounties.dta.
El archivo usacounties_shp.dta es el shapefile
que contiene la información que grmap usará para representar el mapa. No necesitamos
hacer nada con este archivo, pero describamos y enlistemos su contenido para
ver qué contiene.
El shapefile, usacounties_shp.dta, contiene
1,047,409 coordenadas que definen los límites de cada condado en nuestro mapa.
Este archivo también incluye la variable _ID, que se utiliza para
vincular estos datos con los datos en usacounties.dta.
Necesitaremos este archivo más tarde.
A continuación, usemos y describamos el contenido de
usacounties.dta.
Las primeras tres variables contienen información
geográfica sobre cada estado. La variable _ID es el identificador de
unidad espacial para cada condado que se utiliza para vincular este archivo con
el shapefile, usacounties_shp.dta. Las
variables _CX y _CY son las coordenadas x
e y del centroide del área para cada condado. La variable NAME contiene
el nombre del condado para cada observación. La variable GEOID es el
código FIPS almacenado como una cadena. Necesitaremos un código FIPS numérico
para fusionar este conjunto de datos con otros conjuntos de datos a nivel de
condado. Entonces, generemos una variable llamada fips que sea
igual al valor numérico de GEOID.
Guardemos nuestros datos geográficos y pasemos a los
datos COVID-19.
Descargue y prepare los datos del
caso
El archivo time_series_covid19_confirmed_US.csv contiene
datos de series de tiempo para el número de casos confirmados de COVID-19 para
cada condado en los Estados Unidos. Hagamos clic en el nombre del archivo para
ver su contenido.
Cada observación en este archivo contiene los datos
de un condado o territorio en los Estados Unidos. Los recuentos confirmados
para cada fecha se almacenan en variables separadas. Veamos los datos
delimitados por comas haciendo clic en el botón "Raw" junto a la flecha
roja.
Para importar los datos de caso sin procesar, copie
la URL y el nombre de archivo de la barra de direcciones en su navegador web, y
pegue la dirección web en import delimited.
Tenga en cuenta que la URL del archivo de datos es
larga y se ajusta a una segunda y tercera línea en nuestro comando import
delimited. Esta URL debe ser una línea en su comando import delimited.
Describamos este conjunto de datos.
Este conjunto de datos contiene 3,253 observaciones
que contienen información sobre condados en los Estados Unidos. Hagamos una
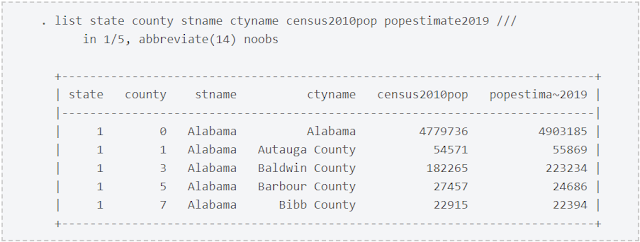
lista de las primeras 10 observaciones para fips, combine_key, v80, v81, v82 y v83.
La variable fips contiene
el código de condado FIPS que usaremos para fusionar este conjunto de datos con
la información geográfica en usacounties_shp.dta. La
variable combine_key contiene el nombre de cada condado y estado en los
Estados Unidos. Y las variables v80, v81, v82 y v83 contienen
el número de casos confirmados de COVID-19 desde el 30 de marzo de 2020 hasta
el 2 de abril de 2020. Los datos de casos más recientes se almacenan en v83, así que
cambiemos su nombre a confirmed.
Encontraremos problemas más adelante cuando
fusionamos conjuntos de datos si fips contiene
valores faltantes. Así que borremos cualquier observación que falte para fips.
Nuestra base de datos COVID-19 está completa.
Guardemos los datos y movámonos a los datos de población.
Descargar y preparar los datos de la
población
Podríamos detenernos aquí, fusionar los datos
geográficos con la cantidad de casos confirmados y crear un mapa coroplético de
la cantidad de casos para cada condado. Pero esto sería engañoso porque las
poblaciones de los condados son diferentes. Podríamos preferir informar la
cantidad de casos por cada 100,000 personas, y eso requeriría conocer la
cantidad de personas en cada condado. Afortunadamente, esos datos están
disponibles en el sitio web de la Oficina del Censo de los
Estados Unidos.
Podemos seguir los mismos pasos que utilizamos para
descargar e importar los datos del caso. Primero, haga clic con el botón
derecho en el nombre del archivo en el sitio web, luego seleccione “Copiar dirección
de enlace” y use import delimited para
importar los datos.
Normalmente describiría el conjunto de datos en este
punto, pero hay 164 variables en este conjunto de datos. Entonces, describiré
solo las variables relevantes a continuación.
La variable census2010pop contiene
la población de cada condado según el censo de 2010. Pero esa información tiene
10 años. La variable popestimate2019 es una
estimación de la población de cada condado en 2019. Usemos esos datos pues son
más recientes.
A continuación, enlistamos los datos.
Este conjunto de datos no incluye una variable con
un código de condado FIPS. Pero podemos crear una variable que contenga el
código FIPS usando las variables state y county. La
inspección visual de los datos geográficos en usacounties.dta indica que
el código FIPS de condado es el código de estado seguido del código de estado
de tres dígitos. Así que creemos nuestra variable de código fips multiplicando
el código state por 1000 y luego agregando el código county.
Hagamos una lista de los datos del condado para
verificar nuestro trabajo.
Este conjunto de datos contiene la población
estimada de cada estado junto con la variable fips que
usaremos como una variable clave para fusionar este archivo de datos con los
otros archivos de datos. Guardemos nuestros datos.
Cómo fusionar los archivos y calcular
recuentos ajustados
Hemos creado tres archivos de datos que contienen la
información que necesitamos para crear nuestro mapa coroplético. El archivo de
datos usacounties.dta contiene la información
geográfica que necesitamos en las variables _ID, _CX y _CY. Recuerde
que estos datos están vinculados al archivo shape, usacounties_shp.dta,
utilizando la variable _ID. El archivo de datos covid19_county.dta contiene
la información sobre el número de casos confirmados de COVID-19 en la variable confirmed. Y el
archivo de datos census_popn.dta contiene
la información sobre la población de cada condado en la variable popestimate2019.
Necesitamos todas estas variables en el mismo
conjunto de datos para crear nuestro mapa. Podemos fusionar estos archivos
usando la variable clave fips.
Comencemos usando solo las variables que necesitamos
de usacounties.dta.
A continuación, combinemos el número de casos
confirmados de covid19_county.dta. La opción
keepusing
(province_state combined_key_confirmed) especifica que fusionaremos solo las variables province_state,
combined_key y confirmed a partir
del archivo de datos covid19_state.dta.
La salida nos dice que 3,142 observaciones tenían
valores coincidentes de fips en los dos
conjuntos de datos. merge también
creó una nueva variable en nuestro conjunto de datos llamada _merge, que
equivale a 3 para observaciones con valores coincidentes de fips.
La salida también nos dice que 91 observaciones
tenían un código fips en los
datos geográficos, pero no en los datos del caso. _merge es igual a
1 para estas observaciones. Hagamos una lista de algunas de estas observaciones.
Las primeras siete observaciones tienen información
geográfica pero no hay datos para confirmed. Vamos a
contar el número de observaciones donde _merge es igual a
1 y done falten los datos de confirmed.
Borremos estas observaciones de nuestro conjunto de
datos pues no contienen datos para confirmed.
La salida de merge también
nos dice que 109 observaciones tenían un código fips en los
datos del caso, pero no en los datos geográficos. _merge es igual a
2 para estas observaciones. Hagamos una lista de algunas de estas observaciones.
Las primeras siete observaciones tienen información
de casos pero no datos para _ID o GEOID.
Algunas de las observaciones son de territorios
estadounidenses que no son estados. Otras observaciones tienen un valor de combined_key
que sugiere
que la información del condado no está clara. La inspección visual de estas
observaciones sugiere que la mayoría de los casos confirmados para estas
observaciones son cero. Podemos verificar esto contando el número de
observaciones donde _merge es igual a
2 y confirmed es igual a
cero.
El resultado indica que 78 de las 109 observaciones
no contienen casos confirmados. Podríamos investigar más estas observaciones si
estuviéramos utilizando nuestros resultados para tomar decisiones políticas.
Pero estas observaciones son una pequeña proporción de nuestro conjunto de
datos, y nuestro objetivo actual es solo aprender a hacer mapas coropléticos.
Así que eliminemos estas observaciones y la variable _merge y sigamos
adelante.
Describamos el conjunto de datos para verificar que
la fusión se realizó correctamente.
A continuación, combinemos la variable popestimate2019 del
archivo de datos census_popn.dta.
La salida nos dice que 3,142 observaciones tenían
valores coincidentes de fips en los dos
conjuntos de datos. merge nuevamente
creó una nueva variable en nuestro conjunto de datos llamada _merge, que es
igual a 3 para observaciones con un valor coincidente de fips.
El resultado también nos dice que 51 observaciones
tenían un código fips en los
datos geográficos, pero no en los datos de la población. _merge es igual a
2 para estas observaciones. Hagamos una lista de algunas de estas
observaciones.
No tenemos información geográfica o de caso para
estas observaciones, por lo tanto, elimínelas de nuestro conjunto de datos y
eliminemos la variable _merge.
Ahora, generemos, etiquetemos y formateemos una
nueva variable llamada confirmed_adj que
contenga el número ajustado por la población de casos confirmados de COVID-19.
Describamos nuestro conjunto de datos para verificar
que contiene todas las variables que necesitaremos para crear nuestro mapa.
Nuestro conjunto de datos está completo! Guardemos el
conjunto de datos y aprendamos cómo crear un mapa coroplético.
Cómo crear el mapa coroplético con
grmap
Utilizaremos el comando grmap, contribuido por la comunidad, para crear nuestro
mapa coroplético. Debe activar grmap antes de usarlo por primera vez.
La creación de un mapa que incluya Alaska y Hawái
requerirá el uso de opciones que se ajusten a su gran diferencia de tamaño y a
que no sean físicamente adyacentes a los otros 48 estados. Me gustaría mantener
nuestro mapa lo más simple posible por ahora, así que voy a borrar las
observaciones de Alaska y Hawai.
A continuación, debemos decirle a Stata que estos
son datos espaciales mediante el uso de spset. La opción modify shpfile(usastates_shp) vinculará
nuestros datos con el shapefile, usastates_shp.dta.
Recuerde
que el shapefile contiene la información que grmap usará para
representar el mapa.
Ahora, podemos usar grmap para crear
un mapa de coropletas para el número de casos confirmados de COVID-19 ajustado
por la población.
Figura 2: Mapa de coropletas usando
sectiles.
Por defecto, grmap divide los
datos en cuatro grupos basados en cuartiles de confirmed_adj. He usado
la opción clnumber(7) para dividir los datos en 7 grupos o sectiles.
Puede cambiar el número de grupos utilizando la opción clnumber(#), donde #
es el número de categorías de colores.
También puede especificar puntos de corte
personalizados utilizando las opciones clmethod(custom) y clbreaks(numlist). El
siguiente mapa utiliza puntos de corte personalizados en 0, 5, 10, 15, 20, 25,
50, 100 y 5000. También he agregado un título y un subtítulo.
Figura 2: Mapa coroplético utilizando
puntos de corte personalizados.
Conclusiones y código recopilado
¡Lo hicimos! ¡Creamos un mapa coroplético del número
ajustado por la población de casos confirmados de COVID-19 en cada condado de
los Estados Unidos! Repasemos los pasos básicos. Primero, descargamos los datos
geográficos de la Oficina del Censo de los
Estados Unidos y los convertimos en archivos de datos Stata usando
spshape2dta. En segundo
lugar, descargamos, importamos y procesamos los datos COVID-19 del repositorio GitHub Johns
Hopkins y los guardamos en un archivo de datos Stata.
En tercer lugar,
descargamos, importamos y procesamos los datos de población de cada condado de
la Oficina del Censo de los
Estados Unidos y los guardamos en un archivo de datos de Stata.
Cuarto, fusionamos los archivos de datos de Stata y calculamos el número de
casos COVID-19 ajustados por la población para cada condado. Y quinto, usamos spset para decirle a Stata que estos son datos
espaciales, y usamos grmap para crear
nuestro mapa coroplético. Puede seguir estos pasos para crear un mapa
coroplético para muchos tipos de datos, para otras subdivisiones de los Estados
Unidos o para otros países.
He recopilado el siguiente código que
reproducirá las figuras 2 y 3.
// Create the geographic datasets
clear
copy https://www2.census.gov/geo/tiger/GENZ2018/shp/cb_2018_us_county_500k.zip
///
cb_2018_us_county_500k.zip
unzipfile cb_2018_us_county_500k.zip
spshape2dta cb_2018_us_county_500k.shp, saving(usacounties) replace
use usacounties.dta, clear
generate fips = real(GEOID)
save usacounties.dta, replace
// Create the COVID-19 case dataset
clear
import delimited
https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_US.csv
rename v83 confirmed
drop if missing(fips)
save covid19_county, replace
// Create the population dataset
clear
import delimited
https://www2.census.gov/programs-surveys/popest/datasets/2010-2019/counties/totals/co-est2019-alldata.csv
generate fips = state*1000 + county
save census_popn, replace
// Merge the datasets
clear
use _ID _CX _CY GEOID fips using usacounties.dta
merge 1:1 fips using covid19_county ///
, keepusing(province_state combined_key
confirmed)
keep if _merge==3
drop _merge
merge 1:1 fips using census_popn ///
, keepusing(census2010pop popestimate2019)
keep if _merge==3
drop _merge
drop if inlist(province_state, "Alaska", "Hawaii")
generate confirmed_adj = 100000*(confirmed/popestimate2019)
label var confirmed_adj "Cases per 100,000"
format %16.0fc confirmed_adj
format %16.0fc confirmed popestimate2019
save covid19_adj, replace
// Create the maps
grmap, activate
spset, modify shpfile(usacounties_shp)
grmap confirmed_adj, clnumber(7)
grmap
confirmed_adj, ///
clnumber(8) ///
clmethod(custom) ///
clbreaks(0 5 10 15 20 25 50 100
5000) ///
title("Confirmed Cases of COVID-19 in the
United States") ///
subtitle("cases per 100,000
population")
Eso es todo por hoy. ¡Gracias por leernos!